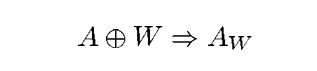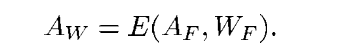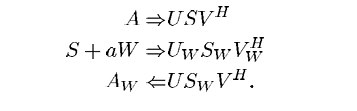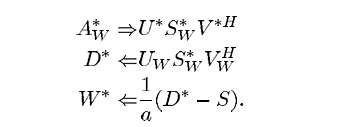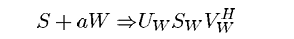无题

An SVD-Based Watermarking Scheme for Protecting Rightful Ownership

一种基于奇异值分解（SVD）的水印方案，用于保护合法所有权

一、翻译

论文翻译阅读–SVD水印（高引用经典论文）

二、解读

不可逆水印

对于图片A，版权所有者使用向其添加水印W，生成带有水印的图片Aw。

攻击者试图生成水印图片的所有权，那么攻击者找到一个虚假的水印Wf和原始图片Af满足水印生成的方案。

算法解析

嵌入过程

1. 首先读取图片A将其进行SVD分解，得到U，S，Vh三个矩阵。
2. 然后将水印图片表示为一个矩阵，添加到奇异值矩阵S中，对新生成的矩阵进行分解得到Sw。
3. 最后，将得到的Sw和第一次SVD分解得到的U和Vh得到带有水印的图片。
4. 保存S和U_w，Vh_w三个矩阵用于提取水印。
   

提取过程

1. 分解带有水印的图片Aw，得到U，S_w和Vh三个矩阵。
2. 用保存的U_w和Vh_w，和第一步得到的S_w计算得到S+aW
3. 得到S+aW后，减去保存的S就可以得到对应的水印W了。
   

不可逆性证明

攻击者想要证明水印图片Aw的所有权，就需要找到新的U_w，Vh_w,，S和水印W使得它们满足嵌入和提取算法。

1. 首先攻击者通过SVD分解水印图片Aw得到U，Sw和Vh。
2. 攻击者得到Sw后，需要设计U_w，Vh_w以及S，W的值，使得下面等式成立。
3. 由于攻击者知道Sw和S的差距不大，所以可以构造一个新的S，这样随机选取一些U_w和Vh_w的值就可以计算出一个水印值W
4. 如果指定水印必须有意义的情况下，攻击者伪造的水印W固定，由于Sw与S接近所以伪造一个S可能可行，但是就难以保证SVD分解出来的对角线元素的Sw。

水印图片对角线像素异常

如果仔细观察可以看到提取的水印图片有一个普遍的特点，对角线元素模糊。

这不是偶然的情况，这是复现的结果：
当我把嵌入强度调高后，这种效果减弱了：
因此猜测是S的对角线奇异值的值很大，而水印图片的值较小，计算时出现的误差。因为我调大嵌入强度，对角线模糊的情况就被改善了

三、代码实现

import cv2
import numpy as np
import matplotlib.pyplot as plt


def svd_watermark_embed(original_img, watermark, alpha=16):
    """
    SVD水印嵌入算法
    :param original_img: 原始图像（灰度）
    :param watermark: 水印矩阵（与图像同尺寸）
    :param alpha: 水印强度系数
    :return: 含水印图像，嵌入用的U_w, S_w, Vh_w
    """
    # 步骤1：对原始图像进行SVD分解
    U, S, Vh = np.linalg.svd(original_img, full_matrices=False)
    S_diag = np.diag(S)

    # 步骤2：将水印加入奇异值矩阵
    watermarked_S = S_diag + alpha * watermark

    # 步骤3：对修改后的矩阵进行SVD分解
    U_w, S_w, Vh_w = np.linalg.svd(watermarked_S, full_matrices=False)
    S_w_diag = np.diag(S_w)

    # 步骤4：生成含水印图像
    watermarked_img = U @ S_w_diag @ Vh

    return np.clip(watermarked_img, 0, 255).astype(np.uint8), (U_w, S, Vh_w)


def svd_watermark_extract(watermarked_img, U_w, Vh_w, original_S, alpha=16):
    """
    SVD水印提取算法
    :param watermarked_img: 含水印图像
    :param U_w: 嵌入时生成的U_w
    :param Vh_w: 嵌入时生成的Vh_w
    :param original_S: 原始图像的奇异值矩阵
    :param alpha: 水印强度系数
    :return: 提取的水印
    """
    # 对含水印图像进行SVD分解
    U_wm, S_wm, Vh_wm = np.linalg.svd(watermarked_img, full_matrices=False)

    # 重建中间矩阵
    D_w = U_w @ np.diag(S_wm) @ Vh_w

    # 提取水印
    extracted_watermark = (D_w - np.diag(original_S)) / alpha

    return extracted_watermark


def watermark_padding(logo, target_size):
    logo = (logo.astype(np.float32) - 128) / 128  # 归一化到[-1,1]范围
    # 目标尺寸
    target_size = min(original.shape)
    # 计算需要填充的像素数
    top = 0
    bottom = target_size - logo.shape[0]
    left = 0
    right = target_size - logo.shape[1]
    # 使用 cv2.copyMakeBorder 进行填充
    padding_logo = cv2.copyMakeBorder(logo, top, bottom, left, right, cv2.BORDER_CONSTANT, value=0)
    return padding_logo


def watermark_resize(logo):
    logo = (logo.astype(np.float32) - 128) / 128  # 归一化到[-1,1]范围
    # 调整尺寸匹配
    resize_logo = cv2.resize(logo, (min(original.shape), min(original.shape)))
    return resize_logo


# 示例使用
if __name__ == "__main__":
    # 读取原始图像并转为灰度
    original = cv2.imread('img/lena.bmp', cv2.IMREAD_GRAYSCALE)

    # 添加语义水印示例
    raw_logo = cv2.imread('img/key_100.png', cv2.IMREAD_GRAYSCALE)
    logo = watermark_padding(raw_logo, min(original.shape))

    # 嵌入语义水印
    watermarked_img, (U_w, S_orig, Vh_w) = svd_watermark_embed(original, logo)

    # 提取水印
    extracted_watermark = svd_watermark_extract(watermarked_img, U_w, Vh_w, S_orig)[:100, :100]

    # 计算相关系数
    correlation = np.corrcoef(raw_logo.flatten(), extracted_watermark.flatten())[0, 1]

    # 可视化结果
    plt.figure(figsize=(10, 5))

    plt.subplot(2, 2, 1), plt.imshow(original, cmap='gray')
    plt.title('Original Image'), plt.axis('off')

    plt.subplot(2, 2, 2), plt.imshow(watermarked_img, cmap='gray')
    plt.title('Watermarked Image'), plt.axis('off')

    plt.subplot(2, 2, 3), plt.imshow(raw_logo, cmap='gray')
    plt.title('Original Watermark'), plt.axis('off')

    plt.subplot(2, 2, 4), plt.imshow(extracted_watermark, cmap='gray', vmin=-1, vmax=1)
    plt.title(f'Extracted Watermark\nCorrelation: {correlation:.4f}'), plt.axis('off')

    plt.tight_layout()
    plt.show()