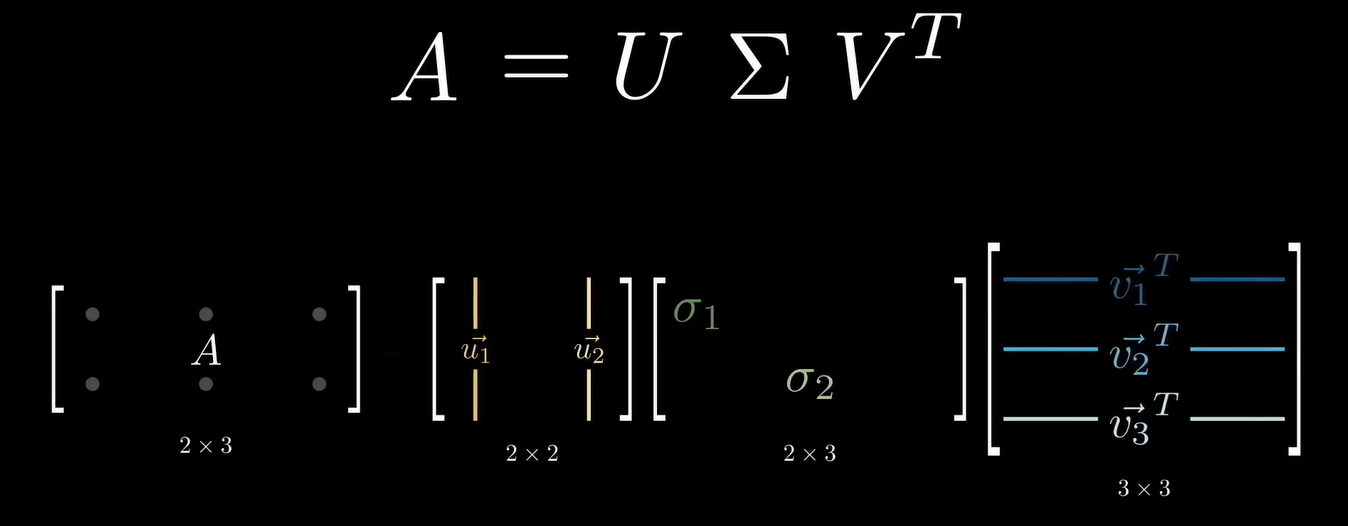无题
奇异值分解(Singular Value Decomposition, SVD)
一、简介
奇异值分解是线性代数中矩阵的一种分解方法,在图像压缩,数据降维和推荐系统等算法中都具有广泛的应用。
与特征值分解不同,它可以应用于长方矩阵中,并将其分解成三个特殊矩阵的乘积。
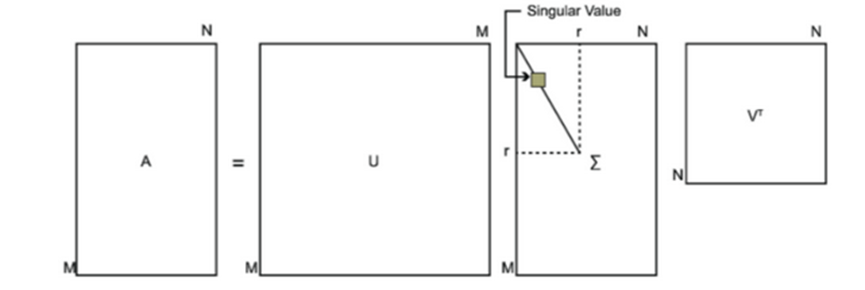
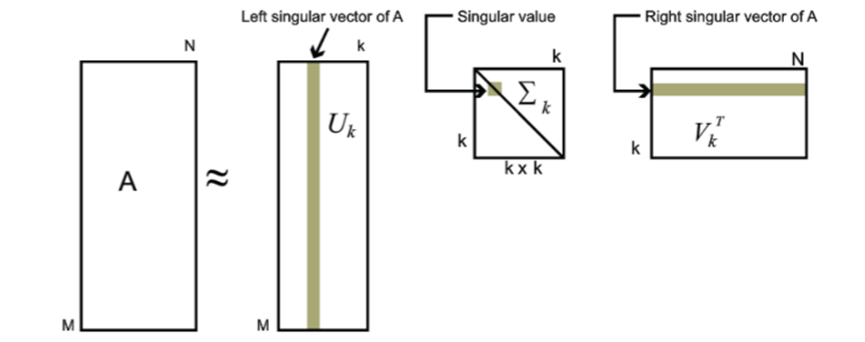
其中U是m×m阶酉矩阵,正交矩阵;Σ是m×n阶非负实数对角矩阵;而Vt,即V的共轭转置,也是正交矩阵,是n×n阶酉矩阵。
这样的分解就称作M的奇异值分解。Σ对角线上的元素Σi,i即为M的奇异值。
二、线性变换视角:旋转+升/降维&&拉伸+旋转
旋转
对于A@A.T和A.T@A两个矩阵,可以很轻易的证明其是对称矩阵。
由于这两个矩阵都是对称矩阵,那么这两个矩阵必然可以进行正交对角化。
计算出左奇异矩阵和右奇异矩阵,这样两个矩阵都代表一种旋转,并且这种旋转不会改变坐标轴的长度。
维度变化
- 维度擦除器
- 维度升高器
拉伸
对于一个对角矩阵,代表这将坐标轴按照指定数字进行拉伸。
拉伸&维度变化
可视化
首先在原始空间进行旋转,变换坐标系
然后将旋转以后得空间进行降维或者上升维度
三、图片压缩视角:秩一矩阵的叠加
任意一张图片可以看做一个矩阵,如果该图片存在多个通道可以将其看做多个矩阵即可。
如果该图片是灰度图,那么可以使用SVD的方法对图片进行分解:
def compress_image(image, k):
"""
对图像进行 SVD 压缩
"""
U, S, Vt = np.linalg.svd(image, full_matrices=False)
compressed_image = U[:, :k] @ np.diag(S[:k]) @ Vt[:k, :]
compressed_image = np.clip(compressed_image, 0, 255) # 限制值范围
return compressed_image
if __name__ == "__main__":
# 读取图片
image_path = '../img/key_100.png'
image = cv2.imread(image_path, 0) # 读取灰度图像
# 检查图片是否成功加载
if image is None:
raise ValueError("图片加载失败,请检查路径是否正确")
# 对图像进行 SVD 压缩
k = 25 # 保留前 k 个奇异值
compressed_image = compress_image(image, k)
k的取值:图片的秩
这里图片的大小为100x100,因此分解的矩阵大小一个是:U100x100,S100,Vt100x100。
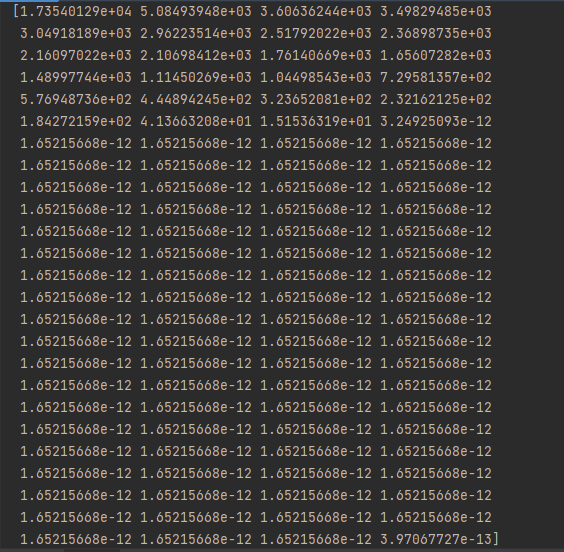
但是,明显的是这张图片显然不像是一个满秩的矩阵,当k取25的时候,可以很好的拟合原始图片。
这里有贡献的k值其实就只有前23位,其后面的数字都极其的小。
这样我们保存了100x25的U矩阵,25的S矩阵,25x100的Vt矩阵,我们仅计算数据量较大的U和Vt矩阵,这样数据量为50x100,为原数据的1/2.
可是,图片却几乎没有受到影响:
k的取值:压缩率
更进一步,可以推导出SVD进行图片压缩的压缩率公式。
假设原始图片的大小为mxn,且m>n,对图片进行SVD变换后,保存k个奇异值。
那么压缩后的U矩阵大小为mxk,S矩阵大小为k,Vt矩阵大小为kxn。因为m>n,所以k最大值为n。
压缩率为:mn/k(m+n+1),当m和n足够大时简化为m*n/k(m+n),那么k需要小于mn/(m+n)。
对于图片是一个方阵的特殊情况,压缩率简化为:nn/k(2n+1)或者当n足够大时:n/2k,可以发现对于方阵要获取有效的压缩k值必须小于n/2。
对于图片长宽比大概为2:1的情况,图片需要保留大约2/3的k值才能进行压缩。对于1920x1080的图片这个值为691。
四、SVD和隐写术
旋转和转置
顺时针旋转90度:将图像顺时针旋转90度后,原矩阵的第i行会变为新矩阵的第(n-1-i)列。
逆时针旋转90度:将图像逆时针旋转90度后,原矩阵的第i行会变为新矩阵的第i列,但顺序反转。
矩阵转置是将矩阵的行和列互换,即原矩阵的第i行第j列元素变为转置矩阵的第j行第i列元素。
顺时针旋转90度:可以看作先对矩阵进行转置,再将转置后的矩阵左右翻转。
逆时针旋转90度:可以看作先将矩阵左右翻转,再进行转置。
图片旋转90度可以通过矩阵转置和翻转操作实现,具体步骤取决于旋转方向。
SVD和旋转
对下面这张图片进行逆时针旋转90度:
得到下面这个图像:
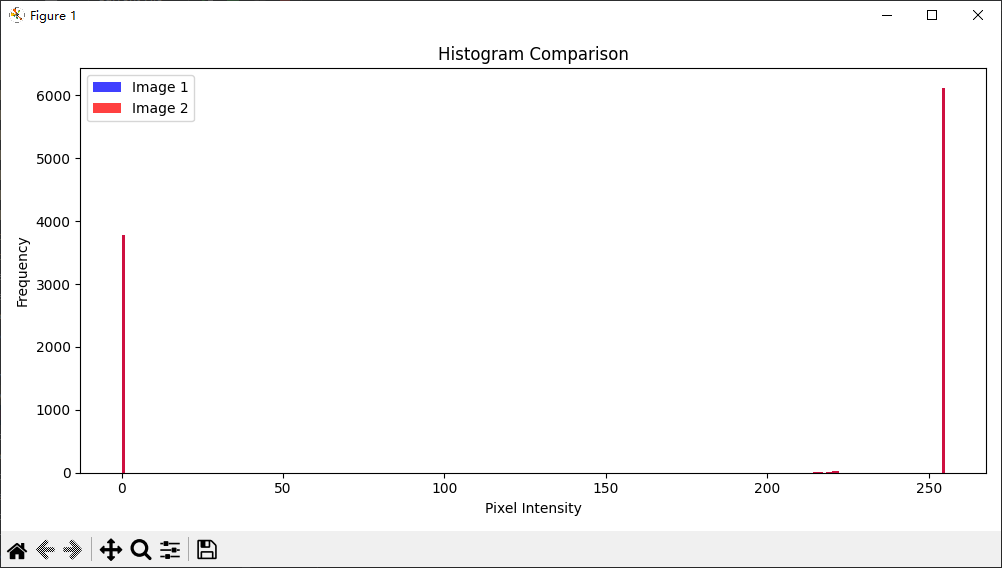
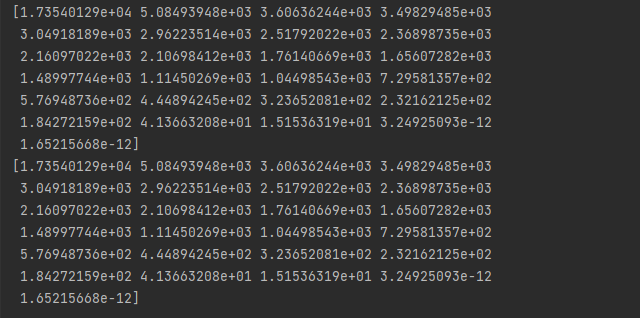
令人震惊的结果是,将图片逆时针旋转90度以后,图像分解的奇异值没有发生任何变化。
原因如下: