图像频域隐写技术:DCT系数隐写
关键词
二值图/灰度图
二值图非常简单,每一个像素使用1比特表示,0代表白,1代表黑。像二维码就可以这样表示节省空间。
灰度图相比于二值图,多了一些介于黑和白之间的灰色,一般每个像素由8比特表示0-255的范围。
黑白电视机放映的就是灰度图像,并不只是黑和白的二值图像。
RGB
RGB是三原色:红Red,绿Green,蓝Blue的英文首字母缩写。
调整三个颜色的比例能够表示其他颜色,就和画图时的调色一样。
在计算机世界,图片由一个个像素点组成,而每个像素点的颜色由RGB表示。
对于一张24位色深的图片,计算机使用24比特表示每个像素的颜色,RGB三个通道各占8比特。因此RGB表示一个像素点就像这样(0,255,0)。
YUV
尽管计算机广泛使用RGB表示颜色并以深入人心,但是YUV的颜色表示方法在工业界应用广泛。
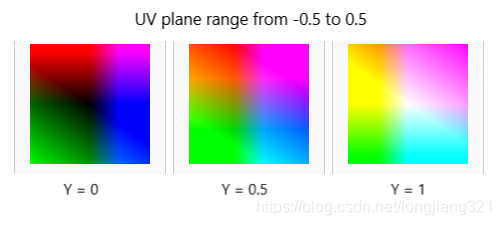
YUV采用明亮度和色度编码颜色,其中Y表示明亮度(Luminance,Luma),而U和V表示色度(Chrominance,Chroma)。其中明度分量可以和色度分量隔离,单独表示一张黑白图片,也就是这点原因YUV可以兼容以前的一些黑白屏幕的设备。另外,由于人眼其实对明度的敏感程度高于色度,因此很多时候,图像处理需要对两个部分做不同处理,比如JPE压缩算法对色度和亮度做了不同方式的压缩。
YUV和RGB也有一些相似的地方,比如G保存了大部分的明度信息,也就是说RGB明度信息是分散的,U和B,V和R的颜色都有相似。你可能能从它们的转化方程中理解这些信息:
如果考虑明度:
Y'= 0.299*R' + 0.587*G' + 0.114*B'
U'= -0.147*R' - 0.289*G' + 0.436*B' = 0.492*(B'- Y')
V'= 0.615*R' - 0.515*G' - 0.100*B' = 0.877*(R'- Y')
R' = Y' + 1.140*V'
G' = Y' - 0.394*U' - 0.581*V'
B' = Y' + 2.032*U'
所以RGB表示的图片和YUV表示的图片都可以转化为一张灰度图片,使用cv2可以轻易完成这个转化过程。
def show_gray(image_path):
# 读取灰度图
gray_image = cv2.imread(image_path, 0)
# 显示
plt.imshow(gray_image, cmap='gray')
plt.title('Gray Image')
plt.show()
# 保存
cv2.imwrite('gray.jpg', gray_image)
时空域/频域
空域是就是我们观测到的世界,每时每刻都在发生着变化。
而频域观点下的世界是不变的,音乐世界的一个音符在空域中表现为一段旋律,而在频域世界它是一个不变的音符,音乐在频域就是众多的音符组成,而在空域就很难定义。
离散余弦变换:DCT
傅里叶变换通过一些列三角函数拟合其他函数,DCT是傅里叶变换的一种特殊方法,用一些列余弦函数拟合离散的波形。
如果把整张图片看做一个波进行DCT变换:
def show_img_dct(img_path):
# 读取灰度图
image = cv2.imread(img_path, 0)
# 进行DCT变换
image_dct = cv2.dct(np.float32(image))
# 显示原图
plt.subplot(1, 2, 1)
plt.imshow(image, cmap='gray')
plt.title('Original Image')
plt.subplot(1, 2, 2)
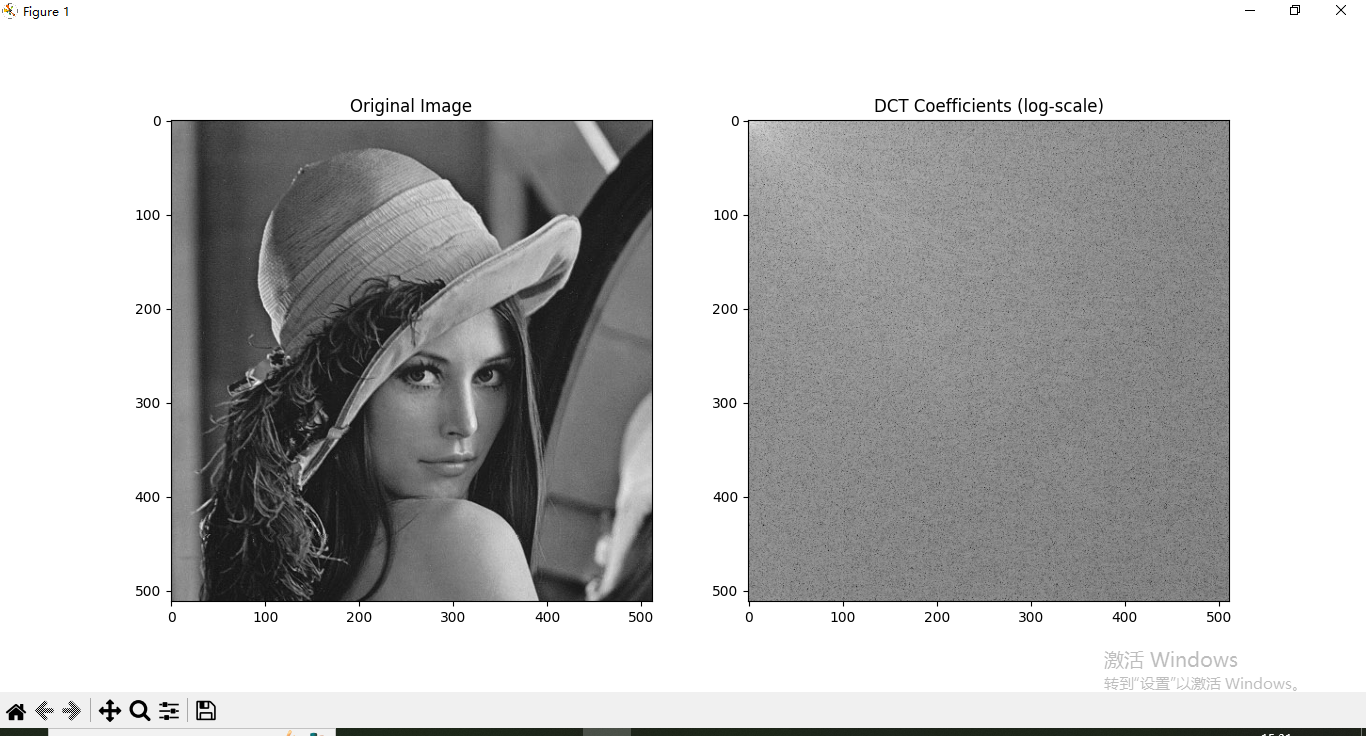
plt.imshow(np.log(abs(image_dct)), cmap='gray')
plt.title('DCT Coefficients (log-scale)')
plt.show()
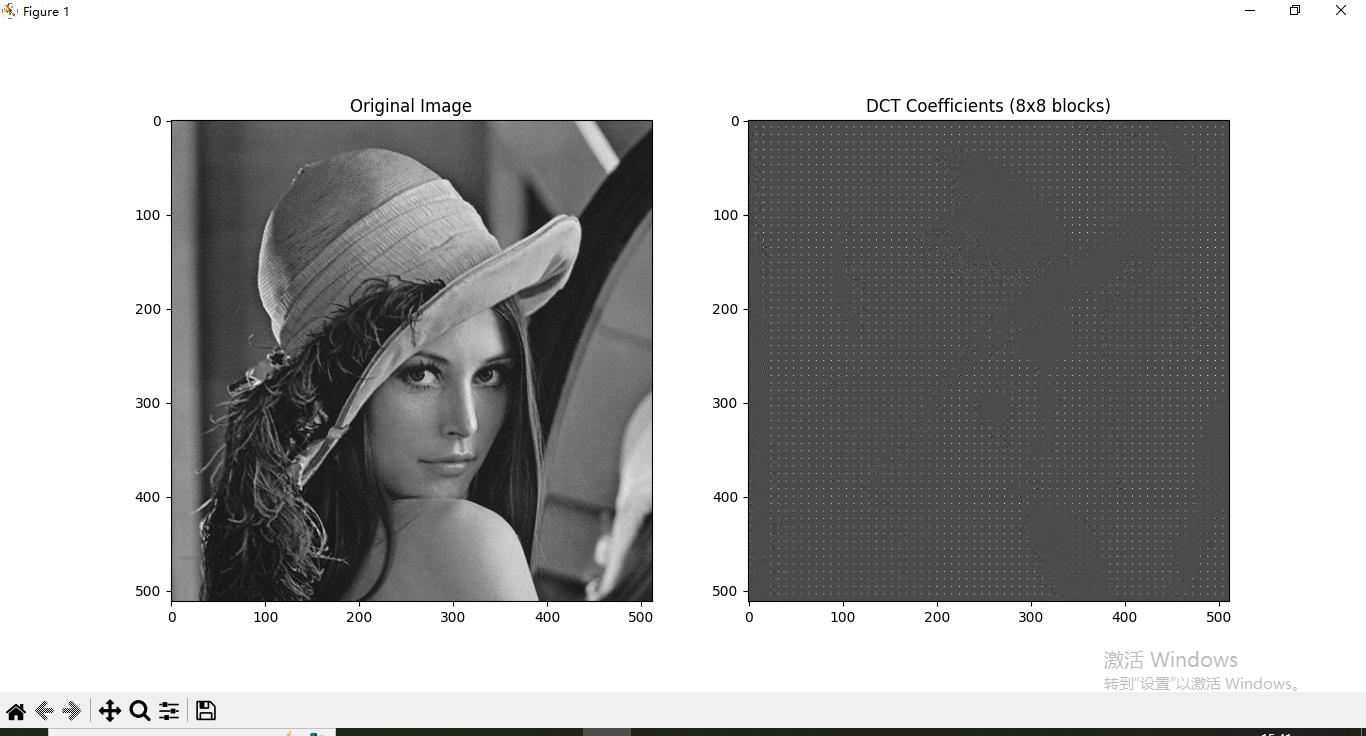
但是很多情况都会对图片进行分块以后DCT变换,特别是JPEG压缩中,并且你可以看到每个8*8小方块总是左上角高亮,这代表左上角低频系数DC有较大的值,其他都是接近0的较小值,这对于JPEG压缩有很大意义。
def show_blocks_dct(image_path):
# 读取灰度图
gray_image = cv2.imread(image_path, 0)
# 对灰度通道进行8x8分块;并进行DCT和量化处理
h, w = gray_image.shape[:2]
blocks_dct = np.zeros((h, w), dtype=np.float32)
for i in range(0, h, 8):
for j in range(0, w, 8):
block = np.float32(gray_image[i:i + 8, j:j + 8] - 128)
block_dct = cv2.dct(block)
blocks_dct[i:i + 8, j:j + 8] = block_dct
# 显示
plt.subplot(1, 2, 1)
plt.imshow(gray_image, cmap='gray')
plt.title('Original Image')
plt.subplot(1, 2, 2)
plt.imshow(blocks_dct, cmap='gray')
plt.title('DCT Coefficients (8x8 blocks)')
plt.show()
JPEG压缩原理
首先将图片从RGB转换为YUV格式进行压缩,因为YUV格式可以更方便的对明度和色度信息进行不同的压缩。
首先对色度信息进行压缩,由于人眼对于颜色没有那么敏感,因此使用采样的方式对图像进行压缩。
另外,对于Y通道进行DCT变换,你会发现对于自然啊图片,DCT的高频系数很多是很小的数字或者零,这是因为自然界的明度变换一般较小并且没有很多分明的轮廓,因此高频系数通常很少,并且大量的高频信息对图片质量影响较小,因此考虑使用一个量化矩阵压缩DCT系数矩阵。这样可以使用哈夫曼编码和游程编码对DCT系数矩阵进行压缩即可,这个步骤通常能够进行10倍的压缩。
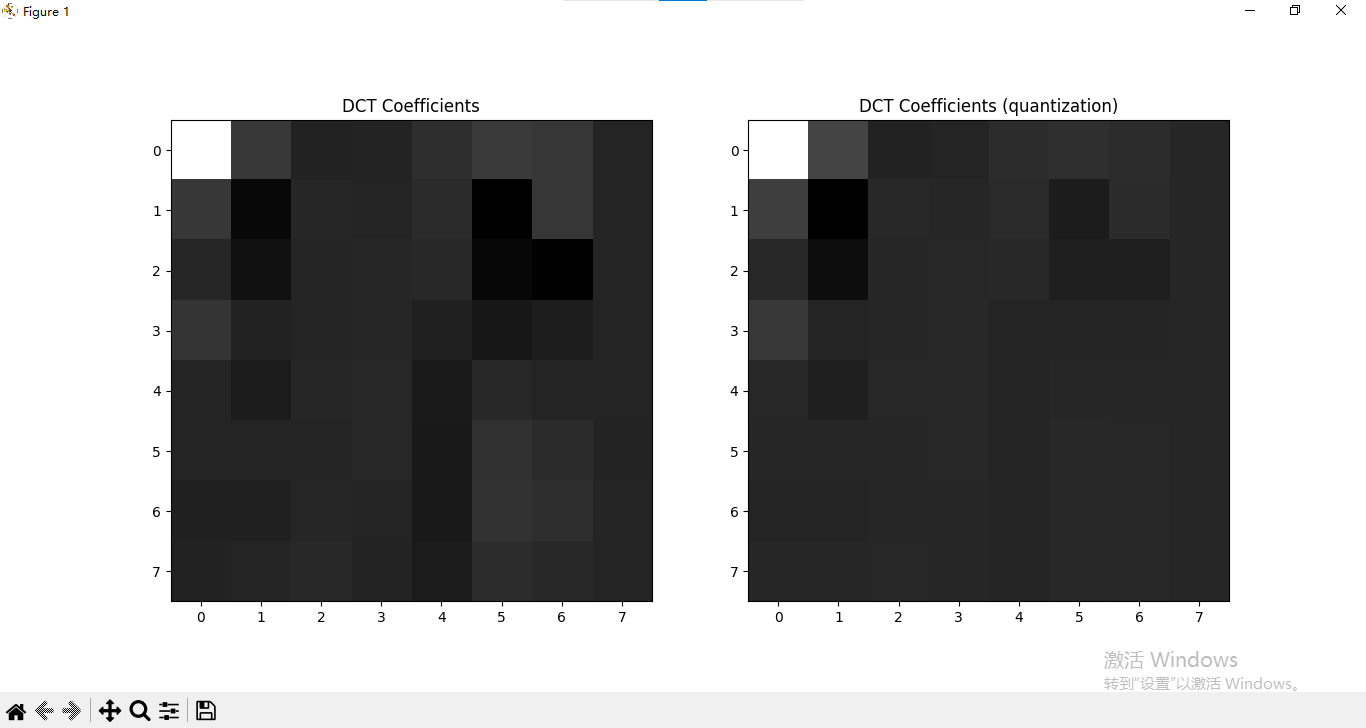
量化矩阵是由压缩实验得出,标准的量化矩阵能够尽可能保证图片质量的情况下最大压缩。你可以看到使用量化矩阵以后较小的高频系数AC都变成了0:
改变i和j的值(i和j必须是8的倍数),你可以看看量化矩阵如何作用于每个8*8分块的DCT系数矩阵,它主要影响右下角的高频系数AC。
# jpg标准量化矩阵
quantization_matrix = np.array([
[16, 11, 10, 16, 24, 40, 51, 61],
[12, 12, 14, 19, 26, 58, 60, 55],
[14, 13, 16, 24, 40, 57, 69, 56],
[14, 17, 22, 29, 51, 87, 80, 62],
[18, 22, 37, 56, 68, 109, 103, 77],
[24, 35, 55, 64, 81, 104, 113, 92],
[49, 64, 78, 87, 103, 121, 120, 101],
[72, 92, 95, 98, 112, 100, 103, 99]
])
def quantization():
# 读取灰度图
gray_image = cv2.imread("lena.bmp", 0)
# 对灰度通道进行8x8分块;并进行DCT和量化处理
h, w = gray_image.shape[:2]
blocks_dct = np.zeros((h, w), dtype=np.float32)
for i in range(0, h, 8):
for j in range(0, w, 8):
block = np.float32(gray_image[i:i + 8, j:j + 8] - 128)
block_dct = cv2.dct(block)
blocks_dct[i:i + 8, j:j + 8] = block_dct / quantization_matrix
if i == 0 and j == 0:
# 显示
plt.subplot(1, 2, 1)
plt.imshow(block_dct, cmap='gray')
plt.title('DCT Coefficients')
plt.subplot(1, 2, 2)
plt.imshow(blocks_dct[i:i + 8, j:j + 8], cmap='gray')
plt.title('DCT Coefficients (quantization)')
plt.show()
然而电脑截图等就会出现很多分明的轮廓,体现到DCT系数就会有很多高频系数并且无法量化为零,这也是为什么JPG对于截图的表现不好而且字体,边界的地方容易糊,因此很多截图实际是使用的PNG格式,PNG格式使用游程编码进行无损压缩,由于电脑截图很多情况下有大量重复像素,因此PNG表现较好。
DCT隐写
LSB隐写有一个很大的缺点就是不能够抗压缩,在网络中图片广泛以JPG格式传输,如果不指定传输原图,大概率会被进行JPG压缩后传输。
在标准量化矩阵量化后的DCT系数矩阵进行隐写,你将得到一个很好的性质,再网络传输中进行量化并不影响隐写内容,如果APP使用标准量化矩阵。
如果能够对量化之后的DCT系数矩阵上进行隐写,那么隐藏在图片上的信息将不会被压缩。如果结合LSB的思想,那么就是广泛使用的Jsteg隐写,以及一些改进比如F3,F4,F5隐写。
另外还有一些广泛使用的方法。
将秘密图片的DCT系数量化后比例叠加到载体图片中,这种方法需要原载体图片才能还原秘密图片。
在中频部分,利用两个位置的DCT系数大小关系进行01编码,如果dct1>dct2表示0,dct1<dct2表示1,如果大小关系不符合则交换两个dct系数的位置。